ベクトル（数C）計算問題１（解答なし）

2024.01.02
数学解説

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Warning: Trying to access array offset on false in /home/xs357883/kashikokunaritai.com/public_html/wp-content/themes/lionblog/functions.php on line 4678

Table of Contents

問1. 次の問いに答えよ。

三角形 $ABC$ において辺 $AB$ を $1:3$ に内分する点を $D$ 、辺 $AC$ を $3:2$ に内分する点を $E$ とする。直線 $CD$ と直線 $BE$ の交点を $F$ とする。

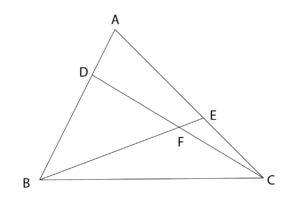
(1) $DF:FC$ および $BF:FE$ を求めよ。

(2) $\overrightarrow{AF}$ を $\overrightarrow{AB}, \overrightarrow{AC}$ で表せ。

(3) 直線 $AF$ と直線 $BC$ の交点を $G$ とする。 $AF:FG$ および $BG:GC$ を求めよ。

問2. 次の問いに答えよ。

三角形 $OCU$ において辺 $OC$ において $OA:AB:BC=1:1:2$ に内分する点 $A,B$ を、辺 $OU$ において $OS:ST:TU=1:2:1$ に内分する点 $S,T$ を図のように定める。直線 $AT$ と直線 $BS$ の交点を $X$ 、直線 $BU$ と直線 $CT$ の交点を $Y$ 、直線 $CS$ と直線 $AU$ の交点を $Z$ とする。

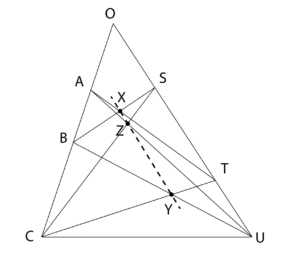
(1) $\overrightarrow{OX},\overrightarrow{OY},\overrightarrow{OZ}$ を $\overrightarrow{OA},\overrightarrow{OS}$ で表せ。

(2) 三点 $X, Y, Z$ が一直線上にあることを示せ。

問3. 次の問いに答えよ。

三角形 $ABC$ は $AB=3,\, BC=5,\, CA=7$ を満たす。三角形 $ABC$ の内心を点 $I$ とする。

(1) $\overrightarrow{AB} \cdot \overrightarrow{AC}$ を求めよ。

2) $\overrightarrow{AI}$ を $\overrightarrow{AB},\,\overrightarrow{AC}$ で表せ。

(3) 線分 $AI$ の長さを求めよ。

(4) 直線 $BC$ に関して、点 $I$ と対称な点を点 $J$ とする。 $\overrightarrow{AJ}$ を $\overrightarrow{AB}, \, \overrightarrow{AC}$ で表せ。

Warning